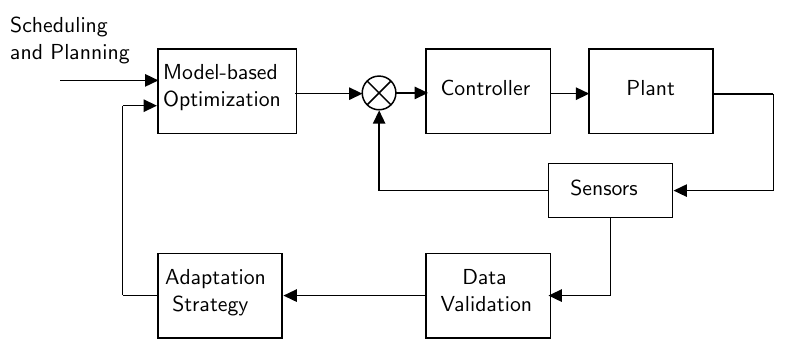
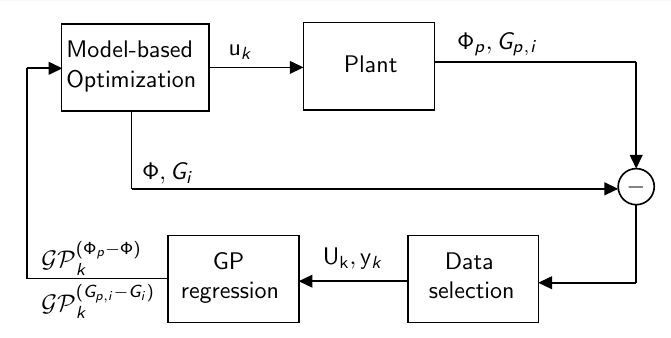
def get_eic_grid(models, xx, yy, f_best):
# unpack stuff
fobj = models['f']
scaler = models['gp_scaler']
constraint0 = models['g_0']
constraint1 = models['g_1']
# flatten each grid to a vector
r1, r2 = xx.flatten(), yy.flatten()
r1, r2 = r1.reshape((len(r1), 1)), r2.reshape((len(r2), 1))
# horizontal stack vectors to create x1,x2 input for the model
grid = np.hstack((r1,r2))
# make predictions for the grid
ei = []
eic = []
g0_probs = []
g1_probs = []
for x in grid:
xs = scaler.transform(x.reshape(1,-1))
model_obj = model.get_objective(x)
model_g = model.get_constraints(x)
adaptation = Bunch(modifiers=[fobj.predict(xs, return_std=True), constraint0.predict(xs, return_std=True), constraint1.predict(xs, return_std=True)])
ei_f = ModelBasedBayesianOptimizer.ei_acquisition(model_obj, adaptation, f_best)
ei.append(ei_f)
probs = ModelBasedBayesianOptimizer.constraint_probability(g, model_g, adaptation)
eic.append(ei_f*np.prod(probs))
g0_probs.append(probs[0])
g1_probs.append(probs[1])
# reshape the predictions back into a grid
zz_ei = np.array(ei).reshape(xx.shape)
zz_g0 = np.array(g0_probs).reshape(xx.shape)
zz_g1 = np.array(g1_probs).reshape(xx.shape)
zz_eic = np.array(eic).reshape(xx.shape)
return zz_ei, zz_g0, zz_g1, zz_eic
def plot_eic_grid(ax, i, best_solutions, gp_iterations, xx, yy, initial_data_size=5):
fbest = best_solutions.iloc[initial_data_size + i]
f_gp, g0_gp, g1_gp, eic = get_eic_grid(gp_iterations[initial_data_size + i],xx,yy,fbest)
plot_decision_surface(fig, ax[0], xx, yy, None, f_gp, 'EI')
plot_decision_surface(fig, ax[1], xx, yy, None, g1_gp*g0_gp, '$Pr(G(x) <= g)$')
plot_decision_surface(fig, ax[2], xx, yy, None, eic, 'EIC')
def plot_eic(i, results, gp_iterations, xx, yy, initial_data_size=5):
fig, ax = plt.subplots(figsize=(10,8))
fbest = results['best_plant_objective'].iloc[initial_data_size + i]
_, _, _, eic = get_eic_grid(gp_iterations[initial_data_size + i],xx,yy,fbest)
plot_decision_surface(fig, ax, xx, yy, None, eic, 'EIC')
ax.scatter(u_plant[0], u_plant[1], c='r', marker='*', s=150, zorder=6)
u_eic = results['u_opt'].iloc[initial_data_size + i]
ax.scatter(u_eic[0], u_eic[1], c='r', marker='x', s=150, zorder=6)
return fig, ax
def plot_eic_iterations(iterations, results, gp_models, initial_data_size=5):
for i, itertrain in enumerate(iterations):
fig, ax = plt.subplots(1,3,figsize=(20,6))
plot_eic_grid(ax, itertrain, results['best_plant_objective'], gp_models,xx,yy)
u_eic = results['u_opt'].iloc[initial_data_size + itertrain]
ax[0].scatter(u_plant[0], u_plant[1], c='r', marker='*', s=150, zorder=6)
ax[1].scatter(u_plant[0], u_plant[1], c='r', marker='*', s=150, zorder=6)
ax[2].scatter(u_plant[0], u_plant[1], c='r', marker='*', s=150, zorder=6)
ax[1].scatter(u_eic[0], u_eic[1], c='r', marker='x', s=150, zorder=6)
ax[2].scatter(u_eic[0], u_eic[1], c='r', marker='x', s=150, zorder=6)
fig.suptitle(f'Iteration: {itertrain}')
fig.show()